


Next: Integraldarstellung in SI-Einheiten
Up: Die Maxwell-Gleichungen
Previous: Die Maxwell-Gleichungen in kovarianter
Aus der kompakten kovarianten Schreibweise der MAXWELL-Gleichungen kann
die übliche differentielle Form leicht abgeleitet werden. Beispielsweise
ergibt sich, wenn man
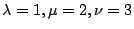 in Gleichung (6)
einsetzt
in Gleichung (6)
einsetzt
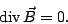 |
(9) |
Die anderen nichtverschwindenden Elemente von (6) liefern analog
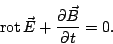 |
(10) |
Die Zerlegung von Gleichung (8) in ihre Komponenten ergibt die
inhomogenen MAXWELL-Gleichungen in der Form
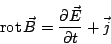 |
(11) |
und
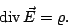 |
(12) |
Damit ist auch die Interpretation der Maxwellgleichungen klar:
- Gleichung (9) besagt, daß keine magnetischen Monopole
existieren.
- Aus Gleichung (12) geht hervor, daß die Quellen des
elektrischen Feldes die Ladungen sind GAUSSsches Gesetz.
- Nach Gleichung (10), dem Induktionsgesetz, ist ein sich
zeitlich änderndes Magnetfeld von einem elektrischen Feld umgeben.
- Das AMPEREsche Gesetz (11) besagt, daß ein zeitlich
veränderliches elektrisches Feld oder ein Strom von einem Magnetfeld
umgeben sind.



Next: Integraldarstellung in SI-Einheiten
Up: Die Maxwell-Gleichungen
Previous: Die Maxwell-Gleichungen in kovarianter
Ulrich Husemann
1998-12-22