


Next: Die Maxwell-Gleichungen in differentieller
Up: Die Maxwell-Gleichungen
Previous: Die Lagrangedichte der QED
Die homogenen MAXWELL-Gleichungen ergeben sich direkt aus der Definition
(4) des Feldstärketensors durch
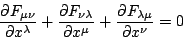 |
(6) |
für
 .
In besonders kompakter Form kann man die
homogenen MAXWELL-Gleichungen mit dem dualen Feldstärketensor
.
In besonders kompakter Form kann man die
homogenen MAXWELL-Gleichungen mit dem dualen Feldstärketensor
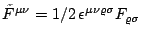 (
(
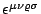 ist dabei das LEVI-CIVITA-Symbol). Sie
lauten dann
ist dabei das LEVI-CIVITA-Symbol). Sie
lauten dann
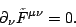 |
(7) |
Die inhomogenen MAXWELL-Gleichungen ergeben sich leicht durch Anwendung
der EULER-LAGRANGE-Gleichung bezüglich  auf die LAGRANGEdichte der QED:
auf die LAGRANGEdichte der QED:
Daraus folgen direkt die inhomogenen MAXWELL-Gleichungen zu:
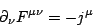 |
(8) |
Ulrich Husemann
1998-12-22