Integraldarstellung in SI-Einheiten

Durch Anwendungen einiger elementarer Sätze der Vektoranalysis lassen sich die MAXWELL-Gleichungen noch in integraler Form darstellen. Ferner gehen wir von den bisher benutzen HEAVISIDE-LORENTZ-Einheiten auf SI-Einheiten über. Aus (9) folgt dann mit dem Satz von GAUSS:

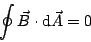$$\oint \vec{B}\cdot\ensuremath{\mathrm{d}}\vec{A}=0$$ (13)

Analog folgt aus (12)

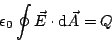$$\epsilon_{0}\oint \vec{E}\cdot\ensuremath{\mathrm{d}}\vec{A}=Q$$ (14)

Benutzt man den Satz von STOKES, so erhält man aus (10) die Form

$$\oint\vec{E}\cdot\ensuremath{\mathrm{d}}\vec{s}=-\frac{\ensu... ...\ensuremath{\mathrm{d}}t}\mbox{ mit }\Phi=\vec{B}\cdot\vec{A}$$ (15)

Analog ergibt sich für (11) die Form

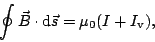$$\oint\vec{B}\cdot\ensuremath{\mathrm{d}}\vec{s}=\mu_{0}(I+I_{\mathrm{v}}),$$ (16)

wobei I_v den MAXWELLschen Verschiebungsstrom bezeichnet. Damit sind die MAXWELL-Gleichungen auf eine praktisch anwendbare Form gebracht.