Die Lagrangedichte der QED

Die LAGRANGEdichte eines freien DIRAC-Spinors $\psi$ schreibt sich bekanntlich als

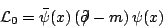$$\mathcal{L}_{0}=\bar\psi(x)\left(\ensuremath{\partial\!\!\!/ }- m\right)\psi(x)$$ (1)

Dabei ist x der Vierervektor $x_{\mu}=(t,\vec{x})$, $\bar\psi=\psi^{\dagger}\gamma_{0}$ die DIRAC-Adjungierte zu $\psi$ und $\ensuremath{\partial\!\!\!/ }=\gamma^{\mu}\partial_{\mu}$. Wie üblich wurden außerdem natürliche Einheiten mit $\hbar=c=1$ benutzt.¹ Mit Hilfe der EULER-LAGRANGE-Gleichung kann man aus Gleichung (1) einfach die DIRAC-Gleichung

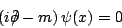$$\left(i\ensuremath{\partial\!\!\!/ }- m\right)\psi(x)=0$$ (2)

ableiten. Diese Theorie hat offensichtlich eine globale U(1)-Symmetrie, das Hinzufügen einer globalen quantenmechanischen Phase zum Spinor in der Form

$$\psi(x)\rightarrow\psi'(x)=e^{i\alpha}\psi(x)$$

ändert also nichts an den physikalischen Observablen. Fordert man aber eine lokale U(1)-Symmetrie der Form

$$\psi(x)\rightarrow\psi'(x)=e^{i\alpha(x)}\psi(x),$$

bei der der Phasenfaktor $\alpha$ eine Funktion von x ist, erfüllt die Theorie diese lokale Eichsymmetrie nur, wenn man in der LAGRANGEdichte die partielle Ableitung $\partial_{\mu}$ durch die sogenannte kovariante Ableitung

$$D_{\mu}=\partial_{\mu}+ieA_{\mu}$$

ersetzt. Dabei wurde ein neues Eichfeld $A_{\mu}$ eingeführt, daß die Transformationseigenschaft

$$A_{\mu}(x)\rightarrow A_{\mu}'(x)=A_{\mu}(x)+\frac{1}{e}\partial_{\mu}\alpha(x)$$

besitzt. Dieses Feld wird später mit den Photonen identifiziert werden. Die Variable e ist ein freier Parameter der Theorie, sie spielt die Rolle der elektrischen Elementarladung. Damit fügt sich in die LAGRANGEdichte ein neuer Wechselwirkungsterm $\mathcal{L}_{\mathrm{WW}}$ ein, so daß

$$\mathcal{L}=\mathcal{L}_{0}+\mathcal{L}_{\mathrm{WW}}=\bar\ps... ...!/ }- m\right)\psi(x)+e\bar\psi(x)\gamma^{\mu} A_{\mu}\psi(x).$$

Der Wechselwirkungsterm kann auch als $-j^{\mu}A_{\mu}$ geschrieben werden, wobei $j^{\mu}$ die Viererstromdichte

$$j^{\mu}=-e\bar\psi(x)\gamma^{\mu}\psi(x)=(\varrho,\vec{j})$$

ist. Wenn man auch den Energieinhalt von $A_{\mu}$ in der LAGRANGEdichte berücksichtigen will, ergibt sich als einziger möglicher LORENTZskalar², der sich aus Ableitungen von $A_{\mu}$ zusammensetzt, die Größe

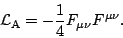$$\mathcal{L}_{\mathrm{A}}=-\frac{1}{4}F_{\mu\nu}F^{\mu\nu}.$$ (3)

Diese Größe beinhaltet den elektromagnetischen Feldstärketensor

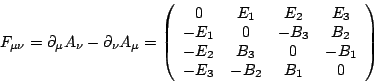$$F_{\mu\nu}=\partial_{\mu}A_{\nu}-\partial_{\nu}A_{\mu}=\left... ...& -B_{1}\\ -E_{3} & -B_{2} & B_{1} & 0 \\ \end{array}\right)$$ (4)

Daraus folgt letztendlich die LAGRANGEdichte der Quantenelektrodynamik (QED) als:

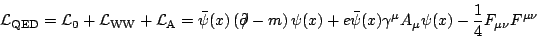$$\mathcal{L}_{\mathrm{QED}}=\mathcal{L}_{0}+\mathcal{L}_{\mat... ...x)\gamma^{\mu} A_{\mu}\psi(x)-\frac{1}{4}F_{\mu\nu}F^{\mu\nu}$$ (5)