Abi-Vorbereitung Kurze Zusammenfassung aller Themen

1. Das e-m Feld

1.1. Vergleich zwischen E- und B-Feld

2. Wechselstrom

2.1. Die Bauelemente des Wechselstroms

2.1.1. Der ohmsche Widerstand

2.1.2. Die Spule

2.1.3. Der Kondensator

2.1.4. Vergleich der Bauelemente

2.1.5. Zusammengesetzte Wechselstromkreise

3. Elektromagnetische Schwingungen

3.1. ungedämfte Schwingungen

3.1.1 Die Meisner-Schaltung (mit Triode)

3.2. Der Transformator

4. Quanten- und Atom-physik

4.1. Wechselwirkung zwischen Licht und Materie

4.1.1. Der Compton-Effekt

4.1.2. Der Photo-Effekt

4.1.3. Die Paarbildung

4.2. Das Termschema des Wasserstoffs

4.2.1. Die Serien

4.3. Moseleysches Gesetz

4.4. Atommodell nach Bohr-Sommerfeld

4.5. Der Franck-Hertz

4.6. Lumineszens

4.6.1. Die Floureszenz

4.6.2. Die Phosphoreszenz

4.7 Klausuraufgabe 2d)

1.1. Vergleich zwischen E- und B-Feld

	E-Feld	B-Feld
Kraftbezeichnung	Coulombkraft	Lorenzkraft
Kraftgleichung:	FE = q * E	FL = q * vs * B
Feldgleichung	E = U/d (homogenes Feld) = 1 / 4peo * Q/r²	B = mr * m0 * H
Ablenkungsfunktion	Parabel	Kreisbahn
Ablenkungsrichtung	in engegengesetzter Ladungsrichtung	um die Magnetlinien gewunden
mechanische Kraft	F = m * a	Fz = m v²/r
Bahngleichung im Feld:	y(x) = eUx²/2dmv0²	y(x) = r-Ö(r²-x²)
unabhängig von:	Bahngleichung v. Elementarladung	Umlaufzeit von Geschwindigkeit

 

2.1. Die Bauelemente des Wechselstroms

2.1.1. Der ohmsche Widerstand

Der ohmsche Widerstand ist frequenzunabhängig. Der Strom folgt der Spannung trägheitsfrei. Für den Ohmschen Widerstand im Wechselstrom gelten die gleichen Gesetze wie im Gleichstrom.

2.1.2. Die Spule

Mit zunehmender Frequenz steigt die Spannung an der Spule, ihr Widerstand wird größer und die Stromstärke sinkt. Der Spulenstromanstieg wird vor der Sättigung abgebrochen. Da die Spannung nach Uind = -L*I' zur Ableitung proportional ist, und die Steigung des I-Graphen gerade im ersten Teil besonders groß ist, nimmt die Spannung zu. Am Anfang des Ladens ist die Spannung hoch und der Strom gering.

2.1.3. Der Kondensator

die Spannung sinkt. Da nach C=Q/U, I=U/t*C der Strom proportional zur Ableitung der Spannung ist und die Steigung des U-Graphen gerade im ersten Teil besonders groß ist, nimmt der Strom zu. Am Anfang des Ladens ist der Stromfluß hoch und die Spannung gering.>

2.1.4. Vergleich der Bauelemente

	Ohmscher Widerstand	Spule	Kondensator
Widerstand in Abhängigkeit der Frequenz	R = konstant	f ~ RL	f ~ 1/RC
Strom zu Spannung	Strom und Spannung in Phase	Strom hinkt Spannung um 90° in der Phase hinterher	Strom eilt Spannung um 90° in der Phase vorraus
Berechnung des Widerstandes	R = U / I	RC = wL	RC = 1/wC

2.1.5. Zusammengesetzte Wechselstromkreise

Den Gesamtwiderstand (Impedanz) Z oder die Gesamtspannung von Blindwiderstand und ohmschen Widerstand bestimmt man Mithilfe eines Zeigerdiagramms. Man trägt die jeweilige Größe mit ihrer der Masszahl entsprechenden Länge und der Phasenverschiebung zu den anderen Größen entsprechenden Winkel in ein rechtwinkliges Koordinatensystem und ermittelt die resultierende Größe und deren Phasenverschiebung phi durch Vektoraddition. Die Phasenverschiebung ist positiv, wenn U I vorauseilt.

Den frequenzunabhängigen ohmschen Widerstand nennt man auch Wirkwiderstand. Dementsprechend Rw, Uw, Iw. Aus den Zeigerdiagrammen ergibt sich beim Hintereinanderschalten von Spule, Kondensator und Wirkwiderstand (Siebkette):

Z = Ö(Rw²+(RL-RC)²);

TAN(j) = (RL-Rc)/Rw;

Im Resonanzfall einer Siebkette sind RL und Rc gleich groß, der zweite Summand im Z-Term fällt weg und der Widerstand ist minimal, nämlich gleich dem Wirkwiderstand. Für den Resonanzfall gilt:

RL = Rc;

Û wL = 1/wC;

Û w² = 1/LC;

Û  f = 1/2pÖ(1/LC);

Unterhalb des Resonanzpunktes werden zu tiefe Frequenzen durch den Kondensator "ausgesiebt", oberhalb zu hohe Frequenzen durch die Spule.

 

Beim Parallelschalten von kapazitivem und induktivem Blindwiderstand (Sperrkreis) zeichnet man das Zeigerdiagramm für I und erhält:

Z = 1/Ö(1/Rw²+(wC-1/wL)²)

TAN(j) = R*(wC-1/wL);

ICundILhaben zu jedem Zeitpunkt verschiedenes Vorzeichen. Sind die Maxima gleich, so wandern die Elektronen beständig im Sperrkreis hin und her. Entlädt sich der Kondensator, so wirkt die Spule dem entgegen und baut ein Magnetfeld auf. Wenn der Kondensator entladen ist, verzögert die Spule ihre Entladung und lädt den Kondensator entgegengesetzt usw (Pumpwirkung).

3.1. ungedämfte Schwingungen

3.1.1 Die Meisner-Schaltung (mit Triode)

Eine Meissnerschaltung (Meissner'sche Rückkopplungsschaltung) besteht aus hintereinandergeschaltetem Sperrkreis und Triode. Eine Triode ist eine Glasröhre mit Vakuum, in der an einem Ende an einer Heizung (Kathode) Elektronen abgedampft werden. Auf der anderen Seite befindet sich eine Anode, zu der die Elektronen beschleunigt werden. Auf halbem Weg befindet sich ein Gitter, das bei negativer Ladung die Elektronen abblockt, sie bei positiver Ladung in Richtung Anode beschleunigt. Jenes Gitter der Triode ist nun an eine Spule angeschlossen ist, die parallel zur Spule des Sperrkreises liegt:

Die Meissnerschaltung sorgt durch Rückkopplung für genau richtig getimten Nachschub für die Schwingung im LC-Glied, es entsteht eine erzwungene ungedämpfte elektromagnetische Schwingung.

Um eine erzwungene e-m-Schwingung zu erzeugen, schaltet man einen unabhängigen Sperrkreis (Sekundärkreis) und legt neben die Spule eine andere Spule, die an einen Wechselstrom angeschlossen wird (Primärkreis). Der Primärkreis regt durch Influenz die Spule des Sperrkreises an und dieser beginnt zu schwingen. Trifft man genau die Resonanzfrequenz, so schwingt der Sperrkreis (fast) ungehindert.

3.2. Der Transformator

Der Transformator besteht aus zwei induktiv gekoppelten Spulen mit den Windungszahlen n1 und n2. Im Transformator wird sowohl Strom (I1) als auch Spannung (U1) am Eingang in neue Größen (I2 und U2) transformiert. Dies geschieht nach folgenden Gesetzmäßigkeiten:

I2eff/I1eff = U1eff/U2eff = n1/n2 (= 1/ü)

Der Transformator ist deshalb im praktischen Leben so wichtig, da der Sekundärkreis problemlos kurzgeschlossen werden kann (I --> ¥), da er nur induktiv gekoppelt ist. Diese Eigenschaft nutzt man beim Elektroschweißen aus.

4.1. Wechselwirkung zwischen Licht und Materie

4.1.1. Der Photo-Effekt

Wir wissen bereits, daß Licht in der Lage ist, Elektronen aus Metall herauszulösen (Compton-Effekt). In diesem Versuch soll nun die Abhängigkeit der kinetischen Energie der herausgelösten Elektronen von der Frequenz des Lichtes ermittelt werden. Zu diesem Zweck wird eine Photozelle beleuchtet. Die Photoezelle besteht aus einer großflächigen Kaliummetallobefläche, vor der sich ein Ring befindet. Auf den Ring soll möglichst wenig Licht treffen. Der Versuch wird nach der Gegenfeldmethode durchgeführt, d.h. die Metalloberfläche wird über eine angeschlossene Niedrigspannungsquelle negativ aufgeladen und der Metallring positiv. Das zwischen dem Metallring und der Metalloberfläche vorhandene elektrische Feld soll von seiner Stärke bei Versuchsbeginn so gering sein, daß trotz des entgegenwirkenden Feldes Elektronen sich von der Metalloberfläche auf den Metallring bewegen. Es soll also ein Strom von der Kaliumschicht zum Ring fließen. Fließt ein Strom, so ist die kinetische Energie der Elektronen höher als die Energie des Feldes. Nach dem Prinzip der Gegenfeldmethode wird nun die anliegende Spannung soweit erhöht, bis kein Strom mehr fließt. Genau dann ist nämlich die Energie des Feldes, die eine abbremsende Kraft auf die Elektronen hervorruft, gleich der maximalen kinetischen Energie der Elektronen. Die so festgestellte Grenzspannung U0 trifft also eine Aussage über die maximale kinetische Energie der herausgelösten Elektronen. Zwischen Spannung und kinetischer Energie gilt folgender Zusammenhang.

Ekin=U*q (Die Probeladung ist in diesem Fall ein Elektron). Man gibt daher die kinetische Energie in Elektronenvolt(eV) an. Ein Elektronenvolt ist die Energie, die ein Elektron beim Durchlaufen einer Strecke mit 1V bekommt.

Es wird definiert: 1ev=1Nm/e (Daher entsprechen sich hier die Werte für Ekin und Uo)

1Joule=1Nm=(10^19)/(1,602 eV)

Benutzt man nun eine Quekssilberdampflampe als Lichtquelle, so kann man mit Hilfe eines Prismas verschiedene Farben als Streifen isolieren. Jede Farbe hat dabei eine andere Frequenz. Mißt bei unterschiedlichen Farben jeweils die Gegenspannug Uo, so erhält man folgenden Graphen.




	gelb	grau	blau	violett
f in 10^14 hz	5,19	5,49	6,88	7,49
Uo in V	0,4	0,55	1,05	1,35
Ekinmax in eV	0,4	0,55	1,05	1,35







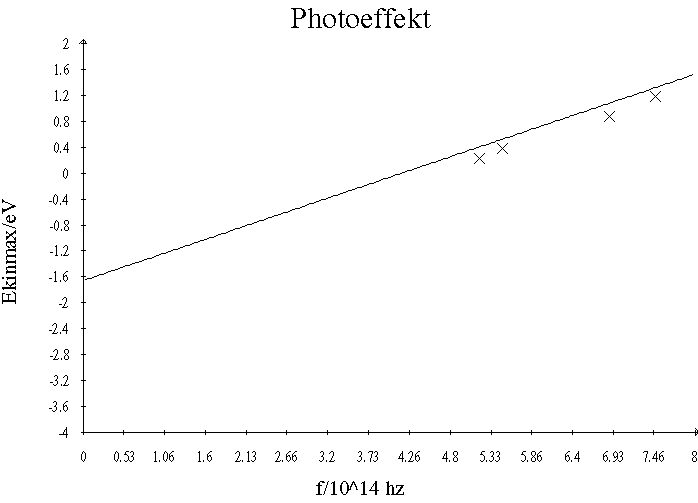
Wie man erkennt, steigt die maximale kinetische Energie der herausgelösten Elektronen proportional mit der Frequenz an. Es gibt außerdem eine Grenzfrequenz fg. Ist die Lichtfrequenz kleiner als diese Grenzfrequenz fg, so werden keine Elektronen herausgelöst, d.h. die kinetische Energie ist kleiner Null. Würde anstatt einer Kaliumplatte eine Zinkplatte verwenden, so würde man einen Graphen mit der gleichen Steigung erhalten. Seine Nullstelle läge lediglich weiter rechts auf der ID-Achse. Bei Zink werden nämlich erst durch ultraviolettes Licht Elektronen herausgelöst. Die Grenzfrequenz hängt also von der Materialart ab. Die Steigung des Graphen kann man mit Hilfe der Meßwerte bestimmen. Es gilt:

Farbe	Gelb	Grau	Blau	Violett
f	5,19	5,49	6,88	7,49
Ekinmax	0,4	0,55	1,05	1,35
Steigung:		0,5	0,36	0,49
Mittelwert Steiung:	0,45
WA	-1,94	-1,92	-2,05	-2,02

Der Idealwert für die Steigung des Graphen isth=0,417*10^-14 eVs. Man nennt h auch das Planksche Wirkungsquantum.




Erklärungstheorien für die Herauslösung der Elektronen aus der Metalloberfläche:

Die klassische Erklärung für diesen Vorgang hat Lenard mit der Wellentheorie geliefert. Nach diesem Modell versetzt das Licht durch seine Energie frei verfügbare Elektronen in der Metalloberfläche in Schwingungen gegenüber seinem Atomrumpf. Sobald ein Elektron genügend Energie durch das Licht aufgenommen hat, kann es die Metalloberfläche mit einer bestimmten kinetischen Energie verlassen. Diese Erklärung steht jedoch nicht in Einklang mit den Versuchsergebnissen überein. Wenn man das Licht als Welle auffaßt hängt nämlich die übertragene Schwingungsenergie, die als Ursache für die Herauslösung angenommen wird, von der Amplitude der Welle und nicht von der Frequenz ab. Im Versuch hat sich jedoch gezeigt, daß die maximale kinetische Energie der Elektronen sowohl von der Intensität des Lichtes als auch von der Bestrahlungsdauer unabhängig ist. Die Existenz einer Grenzfrequenz ist wegen der Unabhängigkeit von der Bestrahlungsdauer damit nicht nachvollziehbar. Nach einer bestimmten Zeit müßte jedes Elektron nämlich genügend Energie gesammelt haben, um die Metalloberfläche zu verlassen. Daher hat man das Erklärungsmodell erweitert. Man nimmt an, daß jede Metalloberfläche eine bestimmte Resonanzfrequenz f hat und erklärt so die Frequenzabhängigkeit. Unverständlich bleibt allerdings auch dann, weshalb die maximale kinetische Energie laut Versuch bei einer Frequenz größer als der Resonanzfrequenz wieder ansteigt. Daraus folgt das die Wellenvorstellung zur Erklärung des Phänomens nicht geeignet ist. Sowohl die Unabhängigkeit von der Intensität und Bestrahlungsdauer als auch das lineare Ansteigen der maximalen kinetischen Energie mit der Frequenz lassen sich nicht erklären.

Einstein hat daher ein grundlegend anderes Erklärungsmodell entwickelt. Er geht davon aus, daß das Licht aus kleinen Energiepaketen besteht (Lichtbündeln, Lichtquanten). Die Energie dieser Lichtbündel hängt von der Frequenz ab. Sie beträgt h*f. Durch die Frequenzabhängigkeit stellt er automatisch einen Zusammenhang mit einem Teil der Wellentheorie her. Er nimmt außerdem an, daß die Lichtquanten sich mit Lichtgeschwindigkeit bewegen und das sie ihre Energie an Elektronen vollständig abgeben können. Er bezeichnet die Lichtquanten im folgenden seiner Theorie als Photonen. Tritt ein solches Photon (es hat die Frequenz des zugehörigen Lichtes) auf ein Leitungselektron in einem Atomverband, so kann das Photon seine gesamte Energie h*f auf das Elektron übertragen. Das Elektron besitzt nun eine bestimmte Energie. Falls diese ausreichend ist, ist das Elektron in der Lage, sich aus dem Atomverband herauszulösen und die Metalloberfläche mit einer bestimmten kinetische Energie zu verlassen. Die zum Verlassen des Atomverbandes notwendige Energie ist abhängig vom Material (der Grenzfrequenz). Bei der Grenzfrequenz ist nämlich die entgegenwirkende Kraft gerade so groß, daß sie die Energie des Elektrons ausgleicht, d.h. das Elektron kann sich zwar aus dem Atomverband lösen, hat danach aber die kinetische Energie Null. Für die Austrittsarbeit WA gilt also: WA=h*fg. Die übertragene Energie spaltet sich also in die für den Austritt benötigte Energie und den Teil, der nach diesem Vorgang als kinetische Energie überbleibt auf.

Es gilt also:

Energie des Photons= (Kinetsiche Energie nach dem Austritt) + (Energie für den Austritt).

Dann gilt für die maximale kinetische Energie nach dem Austritt:

Ekin = h*f - h*fg = h * ( f - fg )

Einsteins Erklärung deckt sich vollständig mit den Versuchsergebnissen. Es stellt sich jedoch die Frage, wie man die anderen Eigenschaften des Lichtes mit Hilfe der Lichtquanten erklären will. Die geradlinige Ausbreitung des Lichtes im Raum, die Inteferenzerscheinungen, die Beugung und die Brechung von Licht decken sich alle mit den bei Wasser festgestellten Eigenschaften und daher mit der Wellentheorie. Man kann natürlich annehmen, daß auch die Lichtquanten alle diese Eigenschaften hat. Man spricht vom Dualismus.

 

4.1.2. Der Compton-Effekt

• Photonen "befreien" mit ihrer Energie hf Elektronen aus Metallen.
• meist mit kurzwelligem Röntgenlicht
• Elektronen werden im Winkel (a) zwischen 0° und 90° abgestoßen
• je kleiner a desto größer die kinetische Energie an das Elektron
• Erhaltungssatz von Energie und Impuls
  • Energieerhaltungssatz:

  WPh + We = WPh' + We' (Satz A)

  • Impulserhaltungssatz:

    pPh^ = pPh'^ + pe^

  nach dem Kosinussatz:

  pe² = pPh² + pPh'² - 2pPh pPh' cos(b) (Satz B)

  • Bekannte Gleichungen:

    1)	WPh = hf = h*c/l	WPh'= hf'= h*c/l'
    2)	We = me * c²	We'= me'* c²
    3)	pPh = WPh/c	pPh'= WPh'/c
    4)	pe = me * v = 0	pe'= me'* v

  • Über Satz B und Gleichung 3) mit c² multipliziert

    pe²*c² = WPh² + WPh'² - 2WPh WPh' cos(b) (5)

  • Aus der Relativitätslehre erhalten wir:

    m = mo * ( 1- v²/c²)

    multipliziert mit:c^4 ( 1- v²/c²) ergibt sich:

    m²c^4 - m²c²v²= mo²c^4

    also:

    Û pe'²*c² = We'² - We² (6)

  • Gleichung (5) in (6):

    We'² - We² = WPh² + WPh'² - 2WPh WPh' cos(b) (7)

  • Satz A in die Gleichung (7) eingesetzt und durch WPh'WPhWe geteilt:

    1/WPh' - 1/WPh = 1/We' (1-cos(b)) (8)

  • (1) in(8)

    Dl = h/me*c (1-cos(b))

    ---

• Wellenlängenzunahme (Dl) ist unabhängig von der eingehenden Wellenlänge !
• Die Comptonwellenlänge (also bei einem Einfallswinkel von 90°) ist 2,4 pm !!
  • lc = h/me*c !!!

4.1.3. Die Paarbildung

• Sonderfall des Comptoneffektes
• ab dem doppelten der Ruheenergie des Elektrons (W =2 me * c² = 1,02 MeV)
• Elektron-Positron (Paar) wird erzeugt.
• nur im Coulombfeld eines Atomkerns möglich
  • --> da sonst nicht gleichzeitig Impuls- und Energieerhaltungssatz gültig wäre.

   

	Photo-Effekt	Compton-Effekt	Paarbildung
Wo?	im Kern	an (freien) Elektronen	im Kern
Was ?	Das Photon überträgt die gesamte Energie auf das Elektron	Das Photon gibt in Abhängigkeit des Streuwinkels einen Teil der Energie an das Elektron ab.	Das Photon erzeugt Positron und Elektron
Wann ?	-	-	bei zweifacher Ruheenergie W=2mec²
Gleichung:	Ee- = EPh	Ee- = EPh (1- ...)	Ee- + Ee+= EPh - 2mec²
Beeinflußung:	keine	keine (W<2mec)	keine (W>2mec)

 

4.2. Das Termschema des Wasserstoffs

4.2.1. Die Serien

Lyman:	f=Ry*(1/1² - 1/n²);
Balmer:	f=Ry*(1/2² - 1/n²)
Paschen:	f=Ry*(1/3² - 1/n²)
Brackett:	f=Ry*(1/4² - 1/n²)
Pfund:	f=Ry*(1/5² - 1/n²)

4.3. Moseleysches Gesetz

• Jedes Element besitzt eine kennzeichnende Röntgenstrahlung
• diese steht mit der Kernladungszahl Z in enger Beziehung
• f ~ ( Z - 1 )
• fnm = [(me e^4 (Z - 1)²) / (8 e0² h³)] * (1/m² - 1/n²)

4.4. Atommodell nach Bohr-Sommerfeld

Nach der Bohr-Sommerfeldschen Theorie gehöhren zu jeder Hauptquantenzahl n Ellipsen verschiedener Exzentrität. Die Bahn mit der Nummer L=n-1 ist dabei kreisförmig. Die halbe Nebenachse der Ellipse ist b = a*(L+1)/n.

Ein Elektron ist durch 4 Quantenzahlen bestimmt:

• Die Hauptquantenzahl n gibt die grosse Halbachse der Ellipse an und damit die Schale: n 1 2 3 4 5 6 Schale K L M N O P
• Die Nebenquantenzahl l entspricht dem Bahndrehimpuls und liegt zwischen 0 und n-1. Sie gibt die "Form" der Atomhülle an. Diese besteht aus luftballonartigen "Orbitalen" (3-dimensionalen Wahrscheinlichkeitswellen), wobei L die Anzahl der Knotenpunkte (REM Komplexität) angibt. Die einzelnen Zustände haben zur Kennzeichnung Buchstaben: L 0 1 2 3 Energiezustand s p d f Zur Hauptquantenzahl 1 gibt es demnach nur den Energiezustand 1s, für n=2 gibt es 2s und 2p usw.
• Die magnetische Quantenzahl m entspricht dem erzeugten Magnetfeld und es gilt: -L <= m <= L. Die Bedeutung der magnetischen Quantenzahl zeigt sich beim Zeemann-Effekt (1895), bei der sich Spektrallinien von Atomen mit L=1 unter Einfluss eines starken Magnetfeldes in 3 Spektrallinien aufspalteten.
• Die Spinquantenzahl s, die die Eigenrotation des Elektrons angibt und die Werte 0.5 und -0.5 annehmen kann. Die Bedeutung der Spinquantenzahl zeigte sich im Stern-Gerlach-Versuch:

Schickt man einen Silber-Atomstrahl durch eine Blende und dann durch das folgende starke Magnetfeld, so spaltet sich der Strahl in 2 Strahlen:

Der Elektronenstrahl geht spektal durch Anordung v und trifft auf einen Schirm. Durch die Eigenrotation (Spin) der Teilchen entsteht ein magnetischer Dipol, der sich entweder senkrecht zum Magnetfeld angeordnet hat oder senkrecht dagegen. Da das Magnetfeld stark inhomogen ist, werden die Teilchen mit dem Südpol oben (starkes Feld) nach unten abgelenkt, die mit dem Nordpol oben hingegen nach oben.

Nach dem Pauli-Prinzip können in einem Atom nie 2 Elektronen in allen Quantenzahlen übereinstimmen. Demnach ergibt sich für die

• K-Schale:

n = 1;

l = 0;

m = 0;

s = ±0.5

2 Elektronen

* L-Schale:

n = 2;

l = 0,1;

m = 0; m = -1,0,1;

s = ±0.5

8 Elektronen

• M-Schale:

  n = 3;

  l = 0,1,2;

  m=0, m = -1,0,1; m = -2,-1,0,1,2;

  s = ±0.5

  18 Elektronen

  Wenn man im Periodensystem der Elemente von einem Element zum nächsten fortschreitet, so bedeutet dies für die die Atomhüllen der neutralen Atome, dass jeweils ein weiteres Elektron eingebaut wird. Die Gesamtzahl der Elektronen ist gleich der Ordnungszahl (Kernladungszahl) Z. Bei Einbau eines neuen Elektrons wird stets die niedrigste noch freie Energiestufe besetzt.

  Die Ordnungszahl ergibt sich als Summe aller Hochzahlen, da diese jeweils die Anzahl der Elektronen pro "Bahn" angeben. Dieses Prinzip gilt bis zur Ordnungszahl 18, da die 4s-Position bei n=19 energetisch tiefer liegt als die 3p- und 3d-Niveaus von n=18.

  Zeichnet man bei der Röntgenbremsstrahlung die Anzahl der Geigerticks in Abhängigkeit vom Winkel nach einer Braggschen Reflexion, so zeigt der Graph, welche Wellenlängen (die ja vom Reflexionswinkel abhängen) in der Röntgenstrahlung zu welchem Anteil vorhanden sind. Es ergibt sich eine Materialunabhängige Kurve (kontinuierliches Bremsspektrum), dem einzelne anodenmaterialabhängige Maxima aufgesetzt sind (die Ka- und Kb-Linie). Moseley fand folgendes Gesetz:

  fk = (Z-a)² Ry (1/n1² - 1/n2²)

  a ist die "Abschirmzahl" 1, die der Tatsache Rechnung trägt, dass nur ein Teil der Kernladung wirksam wird, da der Rest von dem 2. inneren Elektron abgeschirmt wird.

4.5. Der Franck-Herz-Versuch

Beim Franck-Hertz-Versuch wird in eine Triode ein Quecksilberkügelchen (Hg) getan. Sodann wird die Apparatur erhitzt, wobei das Quecksilber verdampft, und der am Auffänger ("oben", ehemals Anode) ankommende Strom in Abhängigkeit von der zwischen Kathode und Gitter (positive Anode) liegenden Spannung gemessen. Zwischen Gitter und Anode liegt eine Vorspannung. Bei ungeheizter Röhre ist bis zu einer gewissen Spannung kein Strom nachzuweisen, da die kinetische Energie der Elektronen (erzeugt durch die Spannung zwischen Kathode und Gitter) nicht ausreicht, um gegen den negativ geladenen Auffänger anzulaufen. Ist die Spannung aber gross genug, so werden die Elektronen genug beschleunigt, um gegen den negativen Auffänger anzulaufen und es fliesst ein konstanter Strom zwischen Kathode und Auffänger.

Wird die Röhre erhitzt, so ist die Röhre voller Quecksilberatome, gegen die die Elektronen unentwegt stossen. Da jedoch die Masse der Elektronen sehr viel kleiner als die der Hg-Atome ist, bleibt es bei elastischen Stössen, bei denen das Elektron keine kinetische Energie verliert: Es fliesst ein Strom.

Wird die Spannung weiter erhöht, so haben die Elektronen auf einmal genug Energie, um mit Hg-Atomen zu wechselwirken: Das Hg-Atom sendet UV-Licht aus und die kinetische Energie des Elektrons sinkt auf 0. Nun reicht die kinetische Energie des Elektrons nicht mehr aus, um gegen den Auffänger anzulaufen, es fliesst weniger Strom. Erhöht man die Spannung weiter, so haben die Elektronen schon im ersten Teil der Röhre genug Energie, um zu wechselwirken; sie tun dieses und werden auf dem Rest der Strecke wieder ausreichend beschleunigt, um einen Strom fliessen zu lassen. Mit wachsender Spannung wechselwirken die Elektronen immer häufiger auf der Strecke zwischen Kathode und Gitter, so dass sich bei jeweils ganz bestimmten Energieniveaus Maxima bilden.

4.6. Lumineszens

4.6.1. Die Floureszenz

• energiereiches (hochfrequentes) Licht hebt ein Elektron auf ein höheres Energieniveau
• dort bleibt es für 10^-7 s
• dann fällt es unter Aussendung eines Photons (niedriger Energie)
• in einen niedrigeres Energieniveau
• letzteres Niveau ist jedoch höher als das ursprüngliche von dem das Elektron stammt
• Die Energie des anregenden Quants muß größer sein, als die des emitierten Quants (Stokesche Regel)

4.6.2. Die Phosphoreszenz

• energiereiches (hochfrequentes) Licht hebt ein Elektron auf ein höheres Energieniveau
• die fällt jedoch nach 10^-8 s wieder in ein weiteres metastabiles Niveau.
• dort bleibt es für 10^-3 s bis einige Minuten
• dann fällt es unter Aussendung eines Photons (niedriger Energie)
• in einen niedrigeres Energieniveau
• Phosphoreszenz wird bei Bildschirmen ausgenutzt.

4.7 Klausuraufgabe 2d)

Zum Nachweis, daß Photonen einen Impuls besitzen, kann der folgende Gedankenversuch dienen: Ein idealreflektierender Spiegel der Masse m 2*10^-5 kg wird an einem dünnen, langen Faden aufgehängt und mit einem kurz dauernden intensiven Lichtblitz der Energie 1 J bestrahlt. Der Spiegel wird dabei wie ein balistisches Pendel ausgelenkt. Wie viele Photonen treffen den Spiegel, wenn l = 693 nm ist ? Bis auf welche Höhe wird der Spiegel dabei ausgelenkt ?

Lösung:

Der Spiegel erfährt bei der Reflektion den doppelten Impuls !

Þ PSpiegel = 2 PLichtblitz(Impulsansatz)

m * v = 2 E/c

Û v = 2*E / m*c (1)

Ausm*g*h = 1/2 mv²erhälth = v²/2g (2)(Pendel)

(1) in (2):

h = 2*E² / m²*c²*g = 5,6 * 10^-9 !!!

(c) by Ph-LK der Marienschule Abi-99